Introducción al Proyecto de Segmentación de Tumores Cerebrales
La segmentación de tumores en imágenes de resonancia magnética es un desafío significativo en el campo de la medicina y la imagenología. La detección precisa y eficiente de tumores es esencial para un diagnóstico adecuado y la planificación de tratamientos, ya que una identificación temprana puede mejorar significativamente las opciones de tratamiento y los resultados para los pacientes.
Este proyecto se centra en el desarrollo de una solución automatizada para la segmentación de tumores en resonancias magnéticas utilizando técnicas avanzadas de procesamiento de imágenes. Los objetivos del proyecto incluyen la implementación de métodos semiautomáticos como Region Growing y Watershed para la identificación y delineación de tumores en imágenes médicas, así como uno automático basado en aprendizaje automático que es UNet.
En particular, se ha utilizado un dataset adaptado del proyecto "Br35H :: Brain Tumor Detection 2020", el cual contiene imágenes de resonancia magnética con anotaciones detalladas para entrenar y evaluar los métodos de segmentación. La implementación en Python de estos métodos se ha llevado a cabo utilizando la librería OpenCV, que proporciona herramientas poderosas para el procesamiento y análisis de imágenes. La segmentación efectiva de tumores puede mejorar la precisión del diagnóstico y apoyar en la toma de decisiones clínicas, contribuyendo así al avance en el cuidado de la salud y la investigación médica.
Métodos y Técnicas
Los métodos semiautomáticos que implementamos en este proyecto son dos:
- Region Growing
- Watershed
La intención detrás de la implementación de estos métodos es lograr identificar el tumor en la resonancia magnética.
En los métodos automáticos se implementara:
- Red Neuronal Convolucional U-Net
Region Growing:
Definición:
Region Growing es una técnica de segmentación de imágenes que consiste en comenzar con un punto semilla inicial (seed point) y ampliar esta región añadiendo píxeles vecinos que cumplan criterios específicos. Este proceso continúa hasta que no haya más píxeles que cumplan los criterios. El objetivo del crecimiento de regiones es dividir una imagen en regiones que sean homogéneas según un criterio de similitud elegido; en nuestro caso, esta región es el tumor.
Implementación del algoritmo:
En nuestro proyecto, la implementación del algoritmo en Python es la siguiente:
def regiongrowing(img, seed, umbral=10):
altura, ancho = img.shape
mascara = np.zeros((altura, ancho), np.uint8)
lista_de_seeds = [seed]
valor_de_seed = img[seed]
while len(lista_de_seeds) > 0:
x, y = lista_de_seeds.pop(0)
if mascara[x, y] == 0:
mascara[x, y] = 255
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if (0 <= x + dx < altura) and (0 <= y + dy < ancho):
if mascara[x + dx, y + dy] == 0 and abs(int(img[x + dx, y + dy]) - int(valor_de_seed)) < umbral:
lista_de_seeds.append((x + dx, y + dy))
return mascara
En particular, es un método que devuelve la máscara tras recibir la imagen, así como una lista de puntos semilla y un umbral para la generación de la región.
Tras generar una imagen vacía del mismo tamaño que la original, aplicamos el algoritmo para el punto semilla y los obtenidos posteriormente, esto es:
- Extraer el valor de intensidad del punto semilla de la imagen, que se utilizará para comparar con los píxeles vecinos
-
Mientras queden píxeles en la lista (que se llena
dinámicamente):
-
Si el píxel no se ha incluido ya en la máscara:
- Marcar el píxel como parte de la región de la máscara
-
Para cada vecino de los 8
- Si se encuentra dentro de los límites de la imagen y si no está ya incluido en la máscara se comprueba si la diferencia de intensidad entre el píxel vecino y el píxel semilla es inferior al umbral definido. En tal caso, se añade el píxel vecino a la lista para su posterior procesamiento.
-
Si el píxel no se ha incluido ya en la máscara:
Este algoritmo se ejecuta en orden O(M⋅N) donde M es el largo en píxeles y N la altura en píxeles.
Watershed
Definición:
La segmentación basada en watershed se basa en considerar la imagen como una topografía donde la intensidad de los píxeles representa la altura. Luego se distinguen los puntos de baja intensidad como valles y los de alta intensidad como picos. Luego se rellenan los valles con agua (de ahí el nombre) logrando segmentar la imagen en distintas regiones. Para su aplicación se debe aplicar un filtro de suavizado a la tomografía e identificar los marcadores iniciales correspondientes a las regiones a segmentar.
Implementación del algoritmo:
En nuestro proyecto, la implementación del algoritmo en Python es la siguiente:
def aplicar_watershed(img):
# Filtro Gaussiano para suavizar la imagen
suavizada = cv2.GaussianBlur(img, (5, 5), 0)
# Resaltar los bordes utilizando la detección de bordes de Canny
bordes = cv2.Canny(suavizada, 100, 200)
# Aplicar la transformación de distancia
dist_transform = cv2.distanceTransform(bordes, cv2.DIST_L2, 5)
# Umbralizar la imagen de distancia para obtener los marcadores
_, marcadores = cv2.threshold(dist_transform, 0.7 * dist_transform.max(), 255, 0)
marcadores = np.uint8(marcadores)
_, marcadores = cv2.connectedComponents(marcadores)
# Aplicar Watershed
marcadores = cv2.watershed(cv2.cvtColor(img, cv2.COLOR_GRAY2BGR), marcadores)
img_watershed = np.copy(img)
img_watershed[marcadores == -1] = 255
return marcadores, img_watershed
En esta implementación hacemos uso de varias funciones de la librería OpenCV donde el desarrollo de las mismas es bastante complejo, en particular nos basamos en el siguiente artículo publicado en Medium por el Ingeniero Jaskaran Bhatia aunque con algunos cambios para nuestra implementación.
Primero hacemos un preprocesamiento a la imagen (el ejemplo
mostrado corresponde a la imagen del dataset y142):
- Se aplica un filtrado gaussiano para suavizar la imagen con kernel 5x5 con el fin de reducir posible ruido.
- Se aplica una detección de bordes utilizando la función Canny de OpenCV, la intención detrás de esto es detectar los bordes en la resonancia, esto debería poder detectar posibles límites para las diversas partes del cerebro y que guíen el proceso de segmentación. El umbral queda seteado entre 100 y 200.
- Transformación de distancia: La intención es calcular la distancia de cada píxel al borde más cercano (detectado en el paso anterior), ayuda a identificar las regiones centrales del tumor pues normalmente son áreas bastante densas y grandes. La función distanceTransform recibe la imagen con los bordes resaltados obtenida anteriormente, un tipo de distancia “DIST_L2” que es la euclidiana y luego un tamaño de máscara 5x5 (se considera una región de 5x5 alrededor de cada píxel al calcular la distancia)
- Umbralización de la imagen de distancia: la intención acá es convertir la imagen a binaria, la función threshold de OpenCV recibe la imagen generada en el paso anterior así como la fórmula de umbralización que es 0.7*dist_transform.max() (cualquier píxel con un valor de distancia superior al 70% de la distancia máxima se setea en 255)
-
Crear los marcadores usando
connectedComponents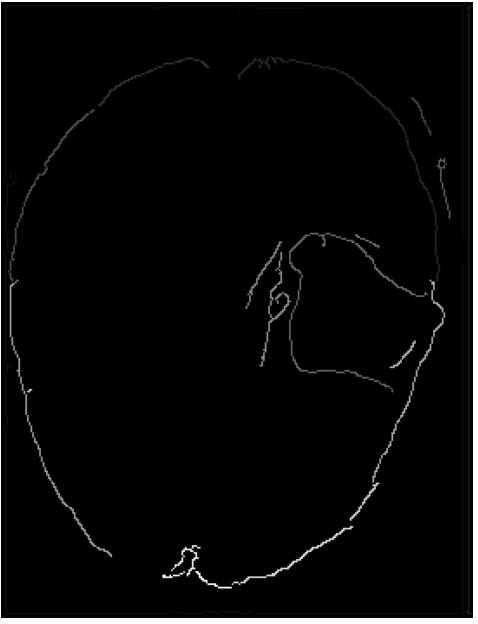

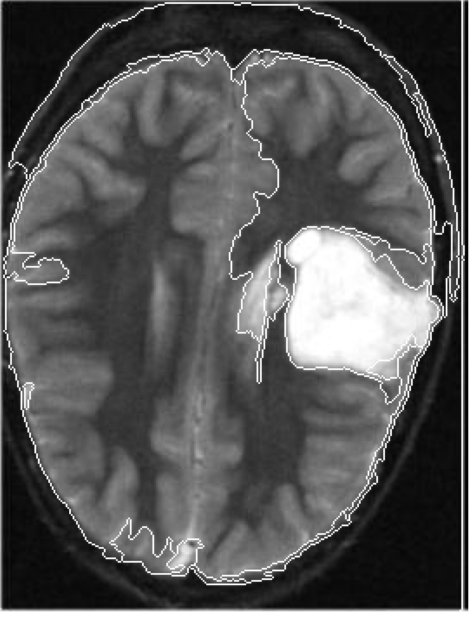 Este algoritmo se ejecuta en orden O(M⋅N) donde M es el largo en
píxeles y N la altura en píxeles. Esto se explica porque cada paso
implica una operación O(M⋅N) en sí, luego, c*O(M⋅N)=O(M⋅N)
Este algoritmo se ejecuta en orden O(M⋅N) donde M es el largo en
píxeles y N la altura en píxeles. Esto se explica porque cada paso
implica una operación O(M⋅N) en sí, luego, c*O(M⋅N)=O(M⋅N)
Implementación interactiva en el proyecto de ambos algoritmos:
Por las características de ambos métodos y del proyecto, decidimos ir por un programa en Python interactivo. La idea inicial era poder mostrar la resonancia al usuario y que, en base a dónde crea que se encuentra el tumor, aplicar el método correspondiente. En particular utilizando utilidades de la librería OpenCV que permiten el manejo de eventos del mouse.
Finalmente decidimos que, en base a la resonancia seleccionada, desplegar dos ventanas:
- Una con la resonancia original (para aplicar Region Growing y crear la máscara)
- Una con las regiones identificadas por Watershed (para crear la máscara en base a la región seleccionada)
Luego se esperan selecciones en ambas ventanas, en particular al menos una por ventana; esto quiere decir que, en caso de tener dos o más tumores, estaría contemplado. Para cada punto de la ventana de Region Growing se ejecuta el algoritmo con ese punto como semilla y, para cada punto seleccionado en la ventana Watershed, se identifica la región donde se encuentra y se agrega la misma a la máscara.
Estos puntos se almacenan en dos listas globales
puntos_original y puntos_watershed,
los clicks en cada ventana se manejan con la siguiente función:
def on_mouse(event, x, y, flags, param):
global puntos_original, puntos_watershed, img, img_watershed, mostrar_resultado
if event == cv2.EVENT_LBUTTONDOWN:
if param == 'original':
puntos_original.append((x, y))
elif param == 'watershed':
puntos_watershed.append((x, y))Luego se setea el callback para cada ventana:
# Ventana original (region growing)
cv2.namedWindow('Imagen Original')
cv2.setMouseCallback('Imagen Original', on_mouse, 'original')
# Ventana watershed (carga la imagen con Watershed ya aplicado)
marcadores, img_watershed = aplicar_watershed(img)
cv2.namedWindow('Watershed')
cv2.setMouseCallback('Watershed', on_mouse, 'watershed')Luego se aguarda que se presione la tecla enter para ejecutar ambos algoritmos si hay puntos seleccionados:
while True:
img_mostrar_original = img_original_color.copy()
img_mostrar_watershed = cv2.cvtColor(img_watershed, cv2.COLOR_GRAY2BGR)
for punto in puntos_original: # Esto dibuja el punto en la ventana
cv2.circle(img_mostrar_original, punto, 3, (0, 255, 0), -1)
for punto in puntos_watershed: # Ídem
cv2.circle(img_mostrar_watershed, punto, 3, (0, 255, 0), -1)
cv2.imshow('Imagen Original', img_mostrar_original)
cv2.imshow('Watershed', img_mostrar_watershed)
tecla = cv2.waitKey(1) & 0xFF
if tecla == 27: # ESC
mostrar_resultado = False
break
elif tecla == 13: # Enter
if len(puntos_original) > 0 and len(puntos_watershed) > 0:
mostrar_resultado = True
breakFinalmente se ejecutan los algoritmos y se muestran las máscaras.
Ejemplo de uso (imagen y142 del dataset):
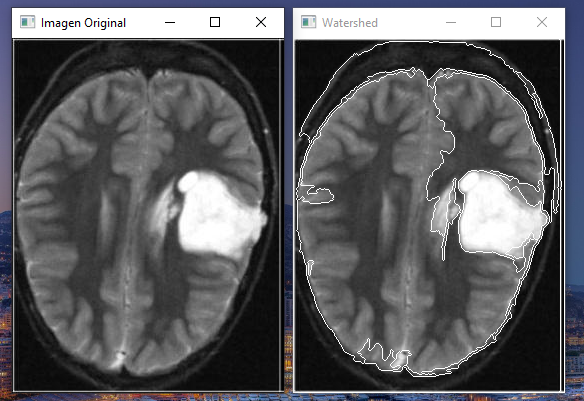
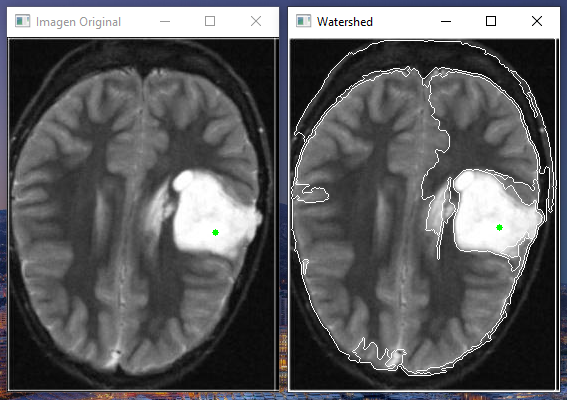

Opcionalmente se pueden guardar las máscaras generadas haciendo uso de la función de OpenCV imwrite.
Region Growing Mejorado
Como resultado de los experimentos realizados quedó en evidencia que el método tiene problemas detectando tumores que son bi-coloridos, es decir, que su núcleo tiene una tonalidad más oscura y su periferia una más clara o viceversa. Esto hace, como vimos que contemos con máscaras como las siguientes:
-
y481
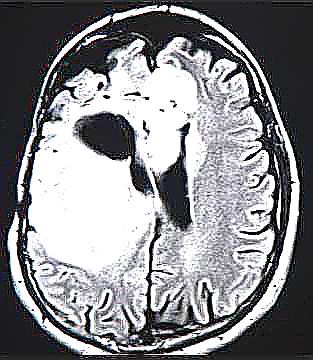
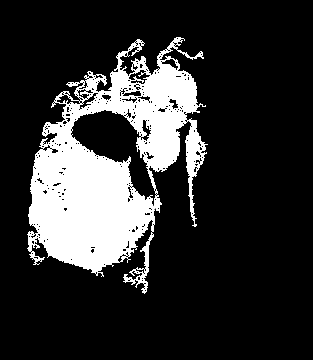
-
y508
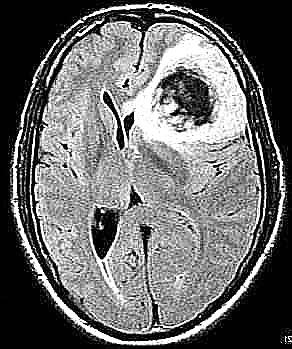

También se pueden observar casos donde existe un solapamiento entre el tumor y el contorno de la cabeza, como la resonancia y538:
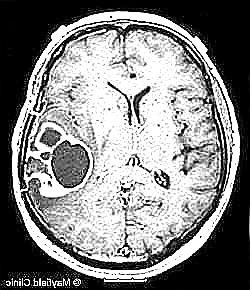
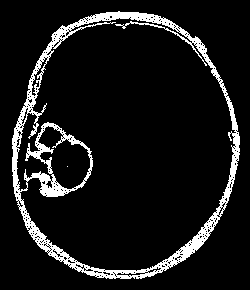
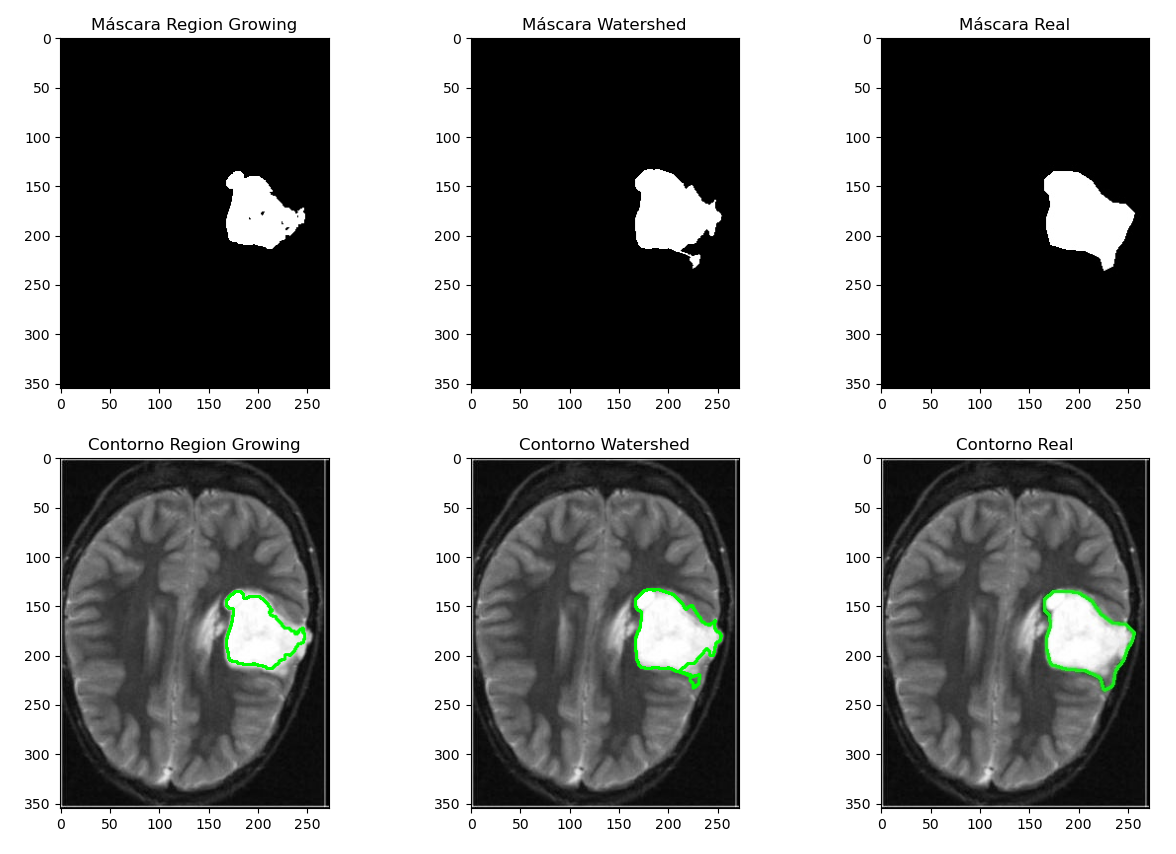
Esto hace que los resultados obtenidos no sean los mejores, aunque el algoritmo no realiza un mal trabajo. Este es el motivo por el cual implementamos el “método de Region Growing mejorado” que detecta el contorno del tumor y lo rellena. Esto hace que obtengamos mejores máscaras: Ejemplo con y481 (máscara region growing, máscara region growing mejorado, máscara real):
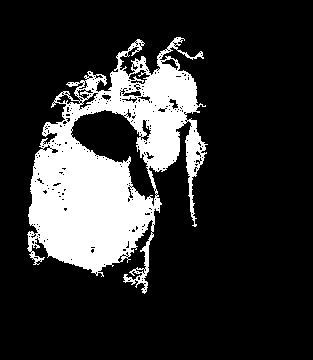


Incluso con la simpleza de la máscara real, es notoria la mejora con este método.
Aún así, puede empeorar máscaras que tienen como contorno la cabeza, en este dataset tenemos solo la y538, en la que obtenemos un peor resultado:

En particular estas nuevas máscaras se pueden obtener haciendo uso de funciones de la librería OpenCV destinadas a la detección de contornos en imágenes como findContours y drawContours.
El algoritmo implementado toma todas las máscaras de region growing y les aplica este procesamiento:
carpeta = 'dataset_final_y_resultados/masks_regiongrowing_mejorado'
def rellenar(mascara):
contornos, _ = cv2.findContours(mascara, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
rellenada = cv2.drawContours(mascara, contornos, -1, 255, thickness=cv2.FILLED)
return rellenada
rg_carpeta = 'dataset_final_y_resultados/masks_regiongrowing'
for mri in os.listdir(rg_carpeta):
mascara = cv2.imread(os.path.join(rg_carpeta, mri), cv2.IMREAD_GRAYSCALE)
rg_mejorado = rellenar(mascara)
ruta_final = os.path.join(carpeta, mri)
cv2.imwrite(ruta_final, rg_mejorado)
En particular el método findContours recibe dos parámetros RETR_EXTERNAL y CHAIN_APPROX_SIMPLE que especifican que sean los contornos externos sean recuperados y el método de aproximación que solo guarda los puntos finales respectivamente.
U-Net
Definición
Una red neuronal U-Net es un tipo de arquitectura de red neuronal convolucional (CNN) diseñada principalmente para realizar tareas de segmentación de imágenes. Fue desarrollada originalmente para segmentar imágenes biomédicas, pero su uso se ha extendido a muchas otras aplicaciones de visión por computadora.
Arquitectura
La arquitectura de U-Net se caracteriza por su forma de "U", que consta de dos partes principales:
-
Contracción (Encoder o Downsampling Path):
- Esta parte de la red realiza la extracción de características.
- Consiste en una serie de capas convolucionales seguidas de capas de pooling (generalmente max pooling), que reducen la resolución de la imagen pero aumentan la cantidad de características.
-
Expansión (Decoder o Upsampling Path):
- Esta parte de la red realiza la reconstrucción de la imagen segmentada.
- Consiste en una serie de capas de upsampling (generalmente transposed convolutions) que aumentan la resolución de la imagen.
- En cada nivel de la expansión, se concatenan las características correspondientes de la parte de contracción a través de conexiones de salto (skip connections), permitiendo que la red recupere información espacial fina que se podría haber perdido durante el proceso de contracción.
Funcionamiento
-
Entrada y Preprocesamiento:
- La imagen de entrada se pasa a través de varias capas convolucionales y de pooling en la fase de contracción.
- Durante este proceso, la red aprende características cada vez más abstractas de la imagen.
-
Bottleneck:
- En el punto más bajo de la "U", se encuentra la parte más densa de la red, donde se encuentran las características más comprimidas y abstractas.
-
Expansión y Segmentación:
- La fase de expansión reconstruye la imagen a su resolución original, pixel a pixel, utilizando las características aprendidas y las conexiones de salto.
- Finalmente, una capa convolucional de salida produce la imagen segmentada, donde cada píxel está clasificado en una de las clases de segmentación.
Implementación del algoritmo
En nuestro el objetivo es obtener un modelo para la predicción de tumores cerebrales en las imágenes de resonancia, a partir de máscaras generadas por el propio modelo Unet y a partir de máscaras reales generadas por otros métodos.
La implementación es mediante la plataforma Python, este es un fragmento del código utilizado:
# Definir el modelo U-Net
def unet_model():
inputs = layers.Input((IMG_HEIGHT, IMG_WIDTH, 1))
s = layers.Lambda(lambda x: x)(inputs) # No normalizar nuevamente aquí
# Contracción
c1 = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(s)
c1 = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(c1)
p1 = layers.MaxPooling2D((2, 2))(c1)
c2 = layers.Conv2D(64, (3, 3), activation='relu', padding='same')(p1)
c2 = layers.Conv2D(64, (3, 3), activation='relu', padding='same')(c2)
p2 = layers.MaxPooling2D((2, 2))(c2)
c3 = layers.Conv2D(128, (3, 3), activation='relu', padding='same')(p2)
c3 = layers.Conv2D(128, (3, 3), activation='relu', padding='same')(c3)
p3 = layers.MaxPooling2D((2, 2))(c3)
c4 = layers.Conv2D(256, (3, 3), activation='relu', padding='same')(p3)
c4 = layers.Conv2D(256, (3, 3), activation='relu', padding='same')(c4)
p4 = layers.MaxPooling2D((2, 2))(c4)
c5 = layers.Conv2D(512, (3, 3), activation='relu', padding='same')(p4)
c5 = layers.Conv2D(512, (3, 3), activation='relu', padding='same')(c5)
# Expansión
u6 = layers.Conv2DTranspose(256, (2, 2), strides=(2, 2), padding='same')(c5)
u6 = layers.concatenate([u6, c4])
c6 = layers.Conv2D(256, (3, 3), activation='relu', padding='same')(u6)
c6 = layers.Conv2D(256, (3, 3), activation='relu', padding='same')(c6)
u7 = layers.Conv2DTranspose(128, (2, 2), strides=(2, 2), padding='same')(c6)
u7 = layers.concatenate([u7, c3])
c7 = layers.Conv2D(128, (3, 3), activation='relu', padding='same')(u7)
c7 = layers.Conv2D(128, (3, 3), activation='relu', padding='same')(c7)
u8 = layers.Conv2DTranspose(64, (2, 2), strides=(2, 2), padding='same')(c7)
u8 = layers.concatenate([u8, c2])
c8 = layers.Conv2D(64, (3, 3), activation='relu', padding='same')(u8)
c8 = layers.Conv2D(64, (3, 3), activation='relu', padding='same')(c8)
u9 = layers.Conv2DTranspose(32, (2, 2), strides=(2, 2), padding='same')(c8)
u9 = layers.concatenate([u9, c1])
c9 = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(u9)
c9 = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(c9)
outputs = layers.Conv2D(1, (1, 1), activation='sigmoid')(c9)
model = models.Model(inputs=[inputs], outputs=[outputs])
return model
Datasets
El dataset a usar es “Br35H :: Brain Tumor Detection 2020” aunque con varias modificaciones. Originalmente este dataset pertenece a una competencia Kaggle (https://www.kaggle.com/datasets/ahmedhamada0/brain-tumor-detection) y tiene dos partes con dos intenciones distintas:
- Una para segmentación
- Una para detección
En este caso nos enfocaremos en el dataset realizado para
segmentación, en particular, el mismo cuenta con un archivo
.json donde se especifican los puntos que conforman los tumores,
así como todas las imágenes de las resonancias magnéticas
correspondientes a los mismos con formato
y%.png donde % corresponde a un número desde el 0
al 800.
Este sub-dataset cuenta con 801 resonancias magnéticas en total, en este proyecto, dadas las características del mismo, lo dividiremos en dos categorías: test y train.
Los métodos de segmentación automáticos usando redes neuronales
serán entrenados con las imágenes desde y0 hasta
y479 y el resto formará parte del conjunto train;
para este último en particular, por la dificultad que conlleva
la aplicación de métodos semiautomáticos, para la aplicación de
Watershed y Region Growing se hará la comparación con las
primeras 60 imágenes, es decir, desde y480 hasta
y539.
Para poder transformar las resonancias magnéticas a las máscaras
utilizando el archivo annotations_all.json dado en
el dataset definimos un script en Python que, mediante el uso de
funciones de la librería OpenCV, dibuja el contorno del tumor y
lo rellena con píxeles blancos bajo una imagen vacía con mismas
dimensiones al MRI original. En particular en este .json
contamos con dos tipos de formas de tumores:
- Polígonos: formados por n puntos
- Elipses: contamos con sus parámetros
Luego basta con definir dos funciones que dibujen estas formas en el plano y rellenar los tumores.
Bloque de código reducido:
# Función para dibujar una elipse
def draw_ellipse(mask, shape_attributes):
center = (int(shape_attributes["cx"]), int(shape_attributes["cy"]))
axes = (int(shape_attributes["rx"]), int(shape_attributes["ry"]))
angle = np.degrees(shape_attributes["theta"])
cv2.ellipse(mask, center, axes, angle, 0, 360, 255, -1)
# Función para dibujar un polígono
def draw_polygon(mask, shape_attributes):
points = np.array(list(zip(shape_attributes["all_points_x"], shape_attributes["all_points_y"])), dtype=np.int32)
cv2.fillPoly(mask, [points], 255)
En particular las funciones draw_polygon y ellipse de OpenCV facilitan esta tarea pues reciben como parámetros los datos que tenemos en el .json dado.
Luego, un elemento estándar de este archivo tiene la forma:
"y102.jpg24000": {
"filename": "y102.jpg",
"size": 24000,
"regions": [
{
"shape_attributes": {
"name": "polygon",
"all_points_x": [
222,
190,
170,
160,
155,
159,
169,
179,
203,
226,
249,
267,
271,
275,
275,
275,
262,
241
],
"all_points_y": [
193,
189,
200,
217,
234,
254,
278,
296,
306,
314,
313,
299,
288,
270,
258,
244,
227,
207
]
},
"region_attributes": {}
}
],
"file_attributes": {}
}
donde en shape_attributes obtenemos el parámetro a customizar, luego para cada ítem de esta colección se crea la máscara:
mask = np.zeros_like(image, dtype=np.uint8)
for region in value['regions']:
shape_attributes = region['shape_attributes']
if shape_attributes['name'] == 'ellipse':
draw_ellipse(mask, shape_attributes)
elif shape_attributes['name'] == 'polygon':
draw_polygon(mask, shape_attributes)
Experimentos
Índice de Jaccard o IoU
El índice de Jaccard o IoU (intersection over union) es una métrica usada para evaluar la eficacia de un método de segmentación en un dataset particular. Calcula el solapamiento entre dos máscaras, una predicha (obtenida con un método de segmentación) y otra real.
La fórmula es:
La siguiente tabla presenta una comparación detallada de los resultados obtenidos a partir de diferentes métodos de segmentación de imágenes de resonancia magnética (MRI) que contienen tumores cerebrales. En esta tabla se evalúan tres métodos de segmentación: Watershed, Region Growing, y Region Growing Mejorado, utilizando dos métricas principales de evaluación: Intersection over Union (IoU) y Dice Coefficient.
Estas métricas se calculan para cada imagen de la base de datos y proporcionan una medida cuantitativa de la precisión y la superposición entre las máscaras de segmentación generadas por los algoritmos y las anotaciones de referencia.
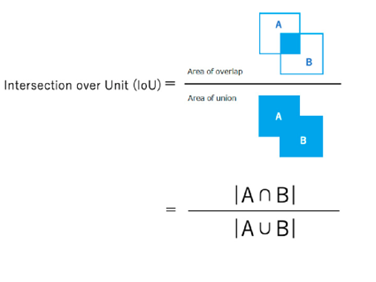
Area of overlap: Es el área donde ambas máscaras coinciden.
Area of union: Es el área total cubierta por ambas máscaras.
Va del 0 al 1 donde el 1 es coincidencia perfecta y 0 sin coincidencia.
Implementación en Python:
def calcular_iou(mascara1, mascara2):
mascara1 = mascara1.astype(bool)
mascara2 = mascara2.astype(bool)
interseccion = np.logical_and(mascara1, mascara2)
union = np.logical_or(mascara1, mascara2)
iou_score = np.sum(interseccion) / np.sum(union)
return iou_score
Como ambas máscaras son binarias, podemos hacer uso de las funciones logical_and y logical_or de numpy donde la primera devuelve los puntos de intersección y la segunda los puntos de unión. Luego la suma de cada uno se usa para devolver el resultado final.
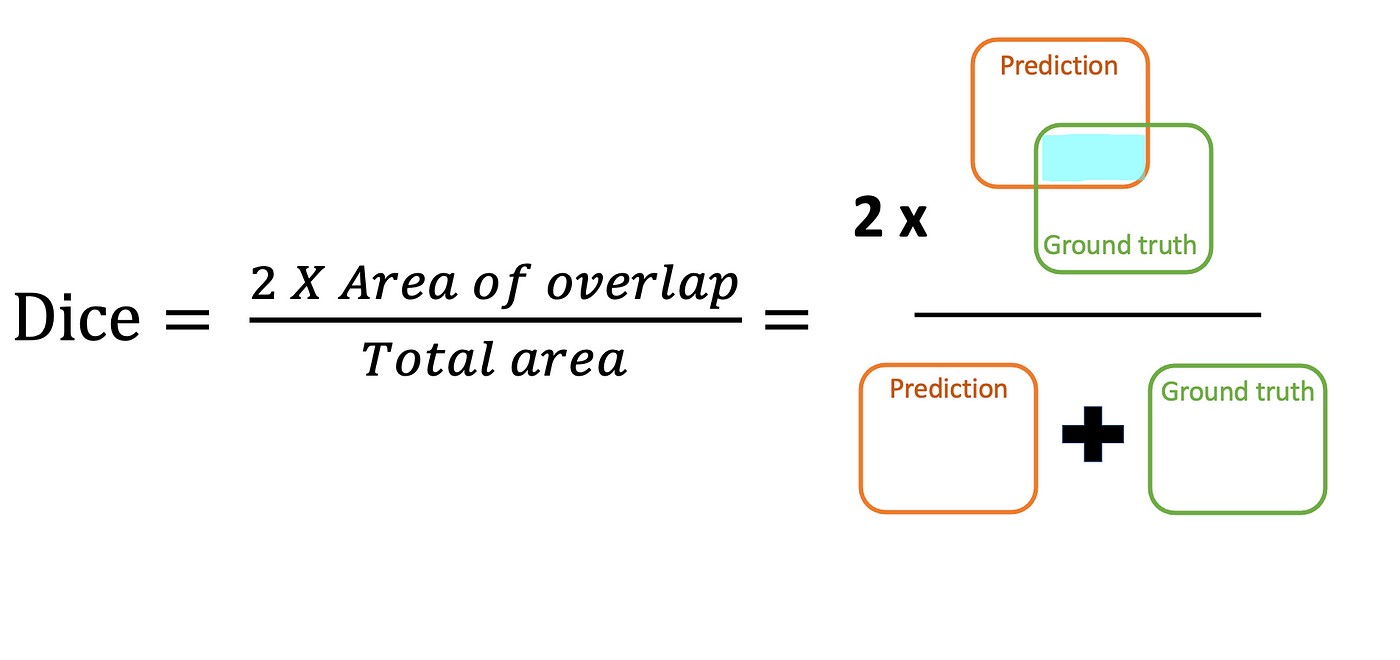
Dice
El coeficiente de Dice (también conocido como F1 score) es una métrica con el mismo fin que IoU, pero su fórmula es distinta:
En este caso hallamos el área de intersección como en IoU pero se duplica y se divide a la suma de las áreas de ambas máscaras.
Luego la implementación en Python es la siguiente:
def calcular_dice(mascara1, mascara2):
mascara1 = mascara1.astype(bool)
mascara2 = mascara2.astype(bool)
interseccion = np.logical_and(mascara1, mascara2)
dice_score = 2 * np.sum(interseccion) / (np.sum(mascara1) + np.sum(mascara2))
return dice_score
 ;
;
Procesamiento
Para procesar los resultados de estos métodos se implementa un script en Python que lee todas las máscaras: las reales, las de region growing, las de region growing mejorado y las de watershed.
En principio tras cargar todas se recorren para poder almacenar los resultados para su posterior análisis haciendo uso de las funciones previamente definidas:
for orig_mascara, w_mascara, rg_mascara, rg_mejorado_mascara in zip(mascaras_originales, mascaras_watershed, mascaras_regiongrowing, mascaras_regiongrowing_mejorado):
iou_watershed = calcular_iou(orig_mascara, w_mascara)
iou_regiongrowing = calcular_iou(orig_mascara, rg_mascara)
iou_regiongrowing_mejorado = calcular_iou(orig_mascara, rg_mejorado_mascara)
dice_watershed = calcular_dice(orig_mascara, w_mascara)
dice_regiongrowing = calcular_dice(orig_mascara, rg_mascara)
dice_regiongrowing_mejorado = calcular_dice(orig_mascara, rg_mejorado_mascara)
resultados_iou['watershed'].append(iou_watershed)
resultados_iou['regiongrowing'].append(iou_regiongrowing)
resultados_iou['regiongrowing_mejorado'].append(iou_regiongrowing_mejorado)
resultados_dice['watershed'].append(dice_watershed)
resultados_dice['regiongrowing'].append(dice_regiongrowing)
resultados_dice['regiongrowing_mejorado'].append(dice_regiongrowing_mejorado)
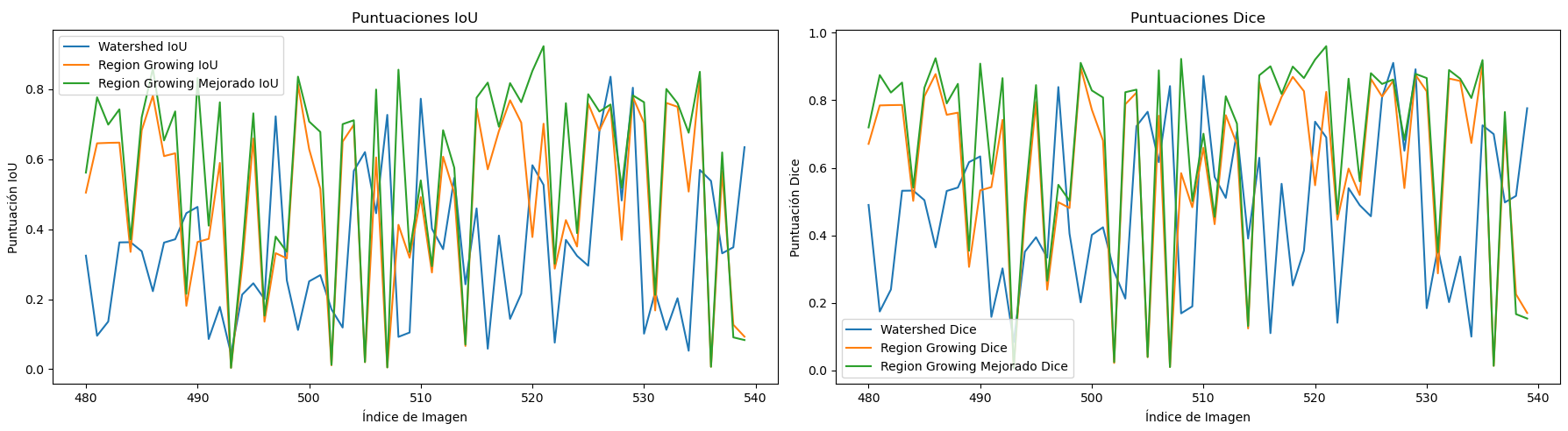
Luego se grafican estos resultados utilizando plots de matplotlib para ambos índices:
x = np.arange(indice_inicio, indice_fin + 1)
plt.figure(figsize=(18, 5))
plt.subplot(1, 2 ,1)
plt.plot(x, resultados_iou['watershed'], label='Watershed IoU')
plt.plot(x, resultados_iou['regiongrowing'], label='Region Growing IoU')
plt.plot(x, resultados_iou['regiongrowing_mejorado'], label='Region Growing Mejorado IoU')
plt.xlabel('Índice de Imagen')
plt.ylabel('Puntuación IoU')
plt.title('Puntuaciones IoU')
plt.legend()
plt.subplot(1, 2, 2)
En particular las variables de índice_inicio e indice_fin indican que parte del dataset queremos analizar.
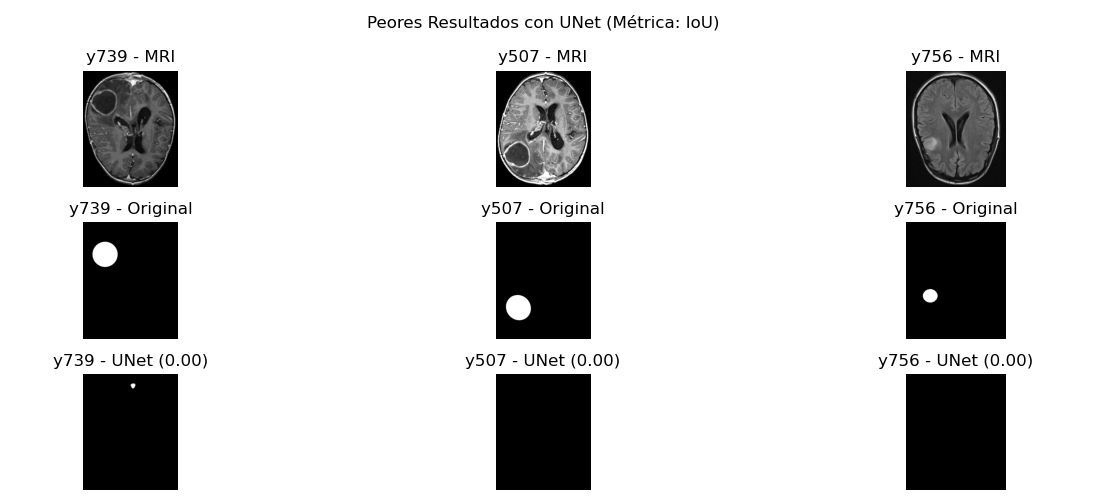
Finalmente tomamos para cada método las 3 resonancias magnéticas donde tuvo peores y mejores resultados ordenando los arreglos previamente almacenados.
Modelo U-Net
En el presente estudio, se ha desarrollado un modelo U-Net para la segmentación de imágenes de resonancia magnética (MRI) con el objetivo de mejorar la precisión en la identificación de estructuras cerebrales y tumores.
Para el entrenamiento y evaluación del modelo, se utilizó un dataset compuesto por 800 imágenes MRI, cada una con sus respectivas máscaras de segmentación. El dataset se dividió en dos conjuntos
- Conjunto de Entrenamiento: Las primeras 480 imágenes y máscaras fueron utilizadas para entrenar el modelo. Este conjunto de datos fue esencial para que el modelo aprendiera a identificar y segmentar las características relevantes en las imágenes.
- Conjunto de Evaluación: Las 320 imágenes restantes fueron empleadas para evaluar el desempeño del modelo una vez completado el entrenamiento. Este conjunto permitió medir la capacidad del modelo para generalizar y realizar segmentaciones precisas en datos no vistos durante el entrenamiento.
El entrenamiento del modelo U-Net se llevó a cabo durante 25 épocas. Durante este proceso, se ajustaron los parámetros del modelo para optimizar su rendimiento en la tarea de segmentación. La elección de 25 épocas fue determinada con base en pruebas preliminares y consideraciones sobre el equilibrio entre tiempo de entrenamiento y el riesgo de sobreajuste.
Conclusiones
Resultados de Segmentación de Tumores Cerebrales
Resultados
| MRI | IOU Watershed | IOU Region Growing | IOU R.G. Mejorado | Dice Watershed | Dice Region Growing | Dice R.G. Mejorado | IOU Unet | Dice Unet | Metodo qué da mejor resultado | Mejor resultado Dice |
| y480.jpg | 0,32 | 0,50 | 0,56 | 0,49 | 0,67 | 0,72 | 0,11 | 0,2 | R.G. Mejorado Dice | 0,72 |
| y481.jpg | 0,10 | 0,65 | 0,78 | 0,17 | 0,78 | 0,87 | 0,5 | 0,67 | R.G. Mejorado Dice | 0,87 |
| y482.jpg | 0,14 | 0,65 | 0,70 | 0,24 | 0,79 | 0,82 | 0,78 | 0,87 | R.G. Mejorado Dice | 0,87 |
| y483.jpg | 0,36 | 0,65 | 0,74 | 0,53 | 0,79 | 0,85 | 0,65 | 0,79 | R.G. Mejorado Dice | 0,85 |
| y484.jpg | 0,36 | 0,34 | 0,37 | 0,53 | 0,50 | 0,54 | 0,22 | 0,37 | R.G. Mejorado Dice | 0,54 |
| y485.jpg | 0,34 | 0,68 | 0,72 | 0,50 | 0,81 | 0,84 | 0,52 | 0,69 | R.G. Mejorado Dice | 0,84 |
| y486.jpg | 0,22 | 0,78 | 0,86 | 0,36 | 0,88 | 0,92 | 0,82 | 0,9 | R.G. Mejorado Dice | 0,92 |
| y487.jpg | 0,36 | 0,61 | 0,65 | 0,53 | 0,76 | 0,79 | 0,64 | 0,78 | R.G. Mejorado Dice | 0,79 |
| y488.jpg | 0,37 | 0,62 | 0,74 | 0,54 | 0,76 | 0,85 | 0,12 | 0,22 | R.G. Mejorado Dice | 0,85 |
| y489.jpg | 0,45 | 0,18 | 0,22 | 0,62 | 0,31 | 0,35 | 0,02 | 0,05 | Watershed Dice | 0,62 |
| y490.jpg | 0,46 | 0,36 | 0,83 | 0,63 | 0,53 | 0,91 | 0,13 | 0,23 | R.G. Mejorado Dice | 0,91 |
| y491.jpg | 0,09 | 0,37 | 0,41 | 0,16 | 0,54 | 0,58 | 0,02 | 0,03 | R.G. Mejorado Dice | 0,58 |
| y492.jpg | 0,18 | 0,59 | 0,76 | 0,30 | 0,74 | 0,87 | 0,66 | 0,8 | R.G. Mejorado Dice | 0,87 |
| y493.jpg | 0,04 | 0,00 | 0,00 | 0,08 | 0,01 | 0,01 | 0,52 | 0,68 | Watershed Dice | 0,68 |
| y494.jpg | 0,21 | 0,29 | 0,33 | 0,35 | 0,46 | 0,50 | 0,61 | 0,76 | R.G. Mejorado Dice | 0,76 |
| y495.jpg | 0,25 | 0,66 | 0,73 | 0,39 | 0,79 | 0,84 | 0,66 | 0,79 | R.G. Mejorado Dice | 0,84 |
| y496.jpg | 0,20 | 0,14 | 0,15 | 0,33 | 0,24 | 0,27 | 0,3 | 0,46 | Watershed Dice | 0,46 |
| y497.jpg | 0,72 | 0,33 | 0,38 | 0,84 | 0,50 | 0,55 | 0,62 | 0,76 | Watershed Dice | 0,84 |
| y498.jpg | 0,25 | 0,32 | 0,34 | 0,41 | 0,48 | 0,50 | 0,67 | 0,81 | R.G. Mejorado Dice | 0,81 |
| y499.jpg | 0,11 | 0,81 | 0,84 | 0,20 | 0,90 | 0,91 | 0,74 | 0,85 | R.G. Mejorado Dice | 0,91 |
| y500.jpg | 0,25 | 0,63 | 0,71 | 0,40 | 0,77 | 0,83 | 0,76 | 0,86 | R.G. Mejorado Dice | 0,86 |
| y501.jpg | 0,27 | 0,52 | 0,68 | 0,42 | 0,68 | 0,81 | 0,59 | 0,74 | R.G. Mejorado Dice | 0,81 |
| y502.jpg | 0,17 | 0,01 | 0,01 | 0,29 | 0,02 | 0,03 | 0,39 | 0,56 | Watershed Dice | 0,56 |
| y503.jpg | 0,12 | 0,65 | 0,70 | 0,21 | 0,79 | 0,82 | 0,55 | 0,71 | R.G. Mejorado Dice | 0,82 |
| y504.jpg | 0,57 | 0,70 | 0,71 | 0,72 | 0,82 | 0,83 | 0,63 | 0,77 | R.G. Mejorado Dice | 0,83 |
| y505.jpg | 0,62 | 0,02 | 0,02 | 0,77 | 0,04 | 0,04 | 0,4 | 0,57 | Watershed Dice | 0,77 |
| y506.jpg | 0,45 | 0,61 | 0,80 | 0,62 | 0,75 | 0,89 | 0,67 | 0,8 | R.G. Mejorado Dice | 0,89 |
| y507.jpg | 0,73 | 0,01 | 0,01 | 0,84 | 0,01 | 0,01 | 0 | 0 | Watershed Dice | 0,84 |
| y508.jpg | 0,09 | 0,41 | 0,86 | 0,17 | 0,58 | 0,92 | 0,44 | 0,62 | R.G. Mejorado Dice | 0,92 |
| y509.jpg | 0,10 | 0,32 | 0,33 | 0,19 | 0,48 | 0,50 | 0,29 | 0,44 | R.G. Mejorado Dice | 0,50 |
| y510.jpg | 0,77 | 0,49 | 0,54 | 0,87 | 0,66 | 0,70 | 0,62 | 0,77 | Watershed Dice | 0,87 |
| y511.jpg | 0,40 | 0,28 | 0,29 | 0,57 | 0,43 | 0,45 | 0 | 0 | Watershed Dice | 0,57 |
| y512.jpg | 0,34 | 0,61 | 0,68 | 0,51 | 0,76 | 0,81 | 0,68 | 0,81 | R.G. Mejorado Dice | 0,81 |
| y513.jpg | 0,55 | 0,50 | 0,58 | 0,71 | 0,67 | 0,73 | 0,73 | 0,85 | R.G. Mejorado Dice | 0,85 |
| y514.jpg | 0,24 | 0,07 | 0,07 | 0,39 | 0,12 | 0,13 | 0 | 0 | Watershed Dice | 0,39 |
| y515.jpg | 0,46 | 0,74 | 0,78 | 0,63 | 0,85 | 0,87 | 0,56 | 0,71 | R.G. Mejorado Dice | 0,87 |
| y516.jpg | 0,06 | 0,57 | 0,82 | 0,11 | 0,73 | 0,90 | 0,24 | 0,38 | R.G. Mejorado Dice | 0,90 |
| y517.jpg | 0,38 | 0,68 | 0,69 | 0,55 | 0,81 | 0,82 | 0,65 | 0,78 | R.G. Mejorado Dice | 0,82 |
| y518.jpg | 0,14 | 0,77 | 0,82 | 0,25 | 0,87 | 0,90 | 0,73 | 0,84 | R.G. Mejorado Dice | 0,90 |
| y519.jpg | 0,22 | 0,70 | 0,76 | 0,35 | 0,83 | 0,87 | 0,51 | 0,68 | R.G. Mejorado Dice | 0,87 |
| y520.jpg | 0,58 | 0,38 | 0,85 | 0,74 | 0,55 | 0,92 | 0,06 | 0,11 | R.G. Mejorado Dice | 0,92 |
| y521.jpg | 0,53 | 0,70 | 0,92 | 0,69 | 0,82 | 0,96 | 0,63 | 0,77 | R.G. Mejorado Dice | 0,96 |
| y522.jpg | 0,08 | 0,29 | 0,30 | 0,14 | 0,45 | 0,46 | 0,38 | 0,55 | R.G. Mejorado Dice | 0,55 |
| y523.jpg | 0,37 | 0,43 | 0,76 | 0,54 | 0,60 | 0,86 | 0,34 | 0,51 | R.G. Mejorado Dice | 0,86 |
| y524.jpg | 0,32 | 0,35 | 0,39 | 0,49 | 0,52 | 0,56 | 0,61 | 0,76 | R.G. Mejorado Dice | 0,76 |
| y525.jpg | 0,30 | 0,76 | 0,79 | 0,46 | 0,86 | 0,88 | 0,58 | 0,73 | R.G. Mejorado Dice | 0,88 |
| y526.jpg | 0,68 | 0,68 | 0,74 | 0,81 | 0,81 | 0,85 | 0,77 | 0,87 | R.G. Mejorado Dice | 0,87 |
| y527.jpg | 0,84 | 0,75 | 0,76 | 0,91 | 0,86 | 0,86 | 0,72 | 0,84 | Watershed Dice | 0,91 |
| y528.jpg | 0,48 | 0,37 | 0,52 | 0,65 | 0,54 | 0,68 | 0,37 | 0,54 | R.G. Mejorado Dice | 0,68 |
| y529.jpg | 0,80 | 0,78 | 0,78 | 0,89 | 0,87 | 0,88 | 0,77 | 0,87 | Watershed Dice | 0,89 |
| y530.jpg | 0,10 | 0,70 | 0,76 | 0,18 | 0,83 | 0,87 | 0,78 | 0,87 | R.G. Mejorado Dice | 0,87 |
| y531.jpg | 0,22 | 0,17 | 0,21 | 0,36 | 0,29 | 0,35 | 0,34 | 0,5 | Watershed Dice | 0,50 |
| y532.jpg | 0,11 | 0,76 | 0,80 | 0,20 | 0,86 | 0,89 | 0,7 | 0,82 | R.G. Mejorado Dice | 0,89 |
| y533.jpg | 0,20 | 0,75 | 0,76 | 0,34 | 0,86 | 0,86 | 0,42 | 0,59 | R.G. Mejorado Dice | 0,86 |
| y534.jpg | 0,05 | 0,51 | 0,68 | 0,10 | 0,67 | 0,81 | 0,48 | 0,65 | R.G. Mejorado Dice | 0,81 |
| y535.jpg | 0,57 | 0,83 | 0,85 | 0,73 | 0,91 | 0,92 | 0,75 | 0,86 | R.G. Mejorado Dice | 0,92 |
| y536.jpg | 0,54 | 0,01 | 0,01 | 0,70 | 0,01 | 0,01 | 0,49 | 0,65 | Watershed Dice | 0,70 |
| y537.jpg | 0,33 | 0,57 | 0,62 | 0,50 | 0,72 | 0,77 | 0,68 | 0,81 | R.G. Mejorado Dice | 0,81 |
| y538.jpg | 0,35 | 0,13 | 0,09 | 0,52 | 0,23 | 0,17 | 0,01 | 0,01 | Watershed Dice | 0,52 |
| y539.jpg | 0,63 | 0,09 | 0,08 | 0,78 | 0,17 | 0,15 | 0,05 | 0,09 | Watershed Dice | 0,78 |
| 0,34 | 0,48 | 0,56 | 0,48 | 0,61 | 0,67 | 0,48 | 0,60 |
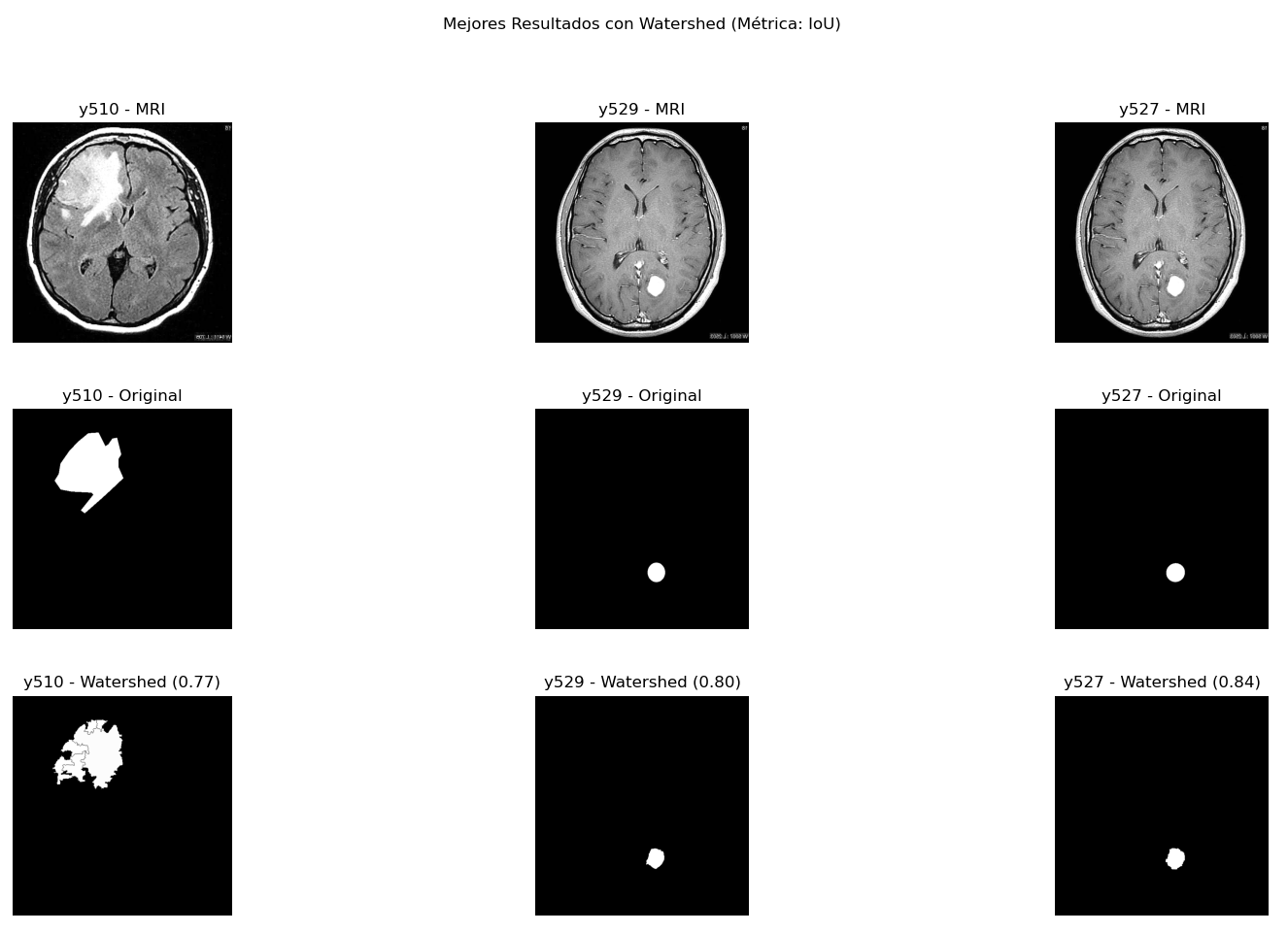
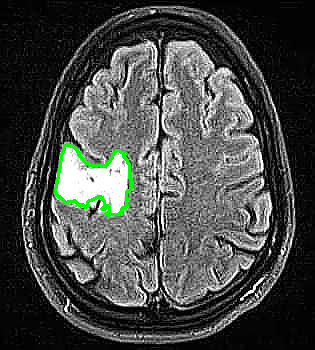
Mejores casos Watershed
Los mejores casos de Watershed ocurren o cuando se pueden seleccionar las regiones que conforman el tumor a la perfección (como el caso del mri y510) o cuando el tumor está muy aislado del resto del cerebro, esto también vamos a ver que es una regla para el método de Region Growing pero es algo relativamente trivial para este método, cuanto más aislado y distinto es el tumor del resto del cerebro más fácil es para el algoritmo poder identificarlo como una región aislada (ya que detecta los bordes facilmente) y luego se obtiene una máscara casi perfecta. Ejemplos y526 (dice 81%) y y528 (dice 65%).
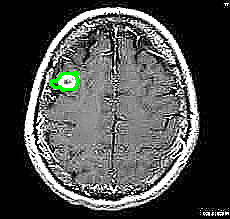
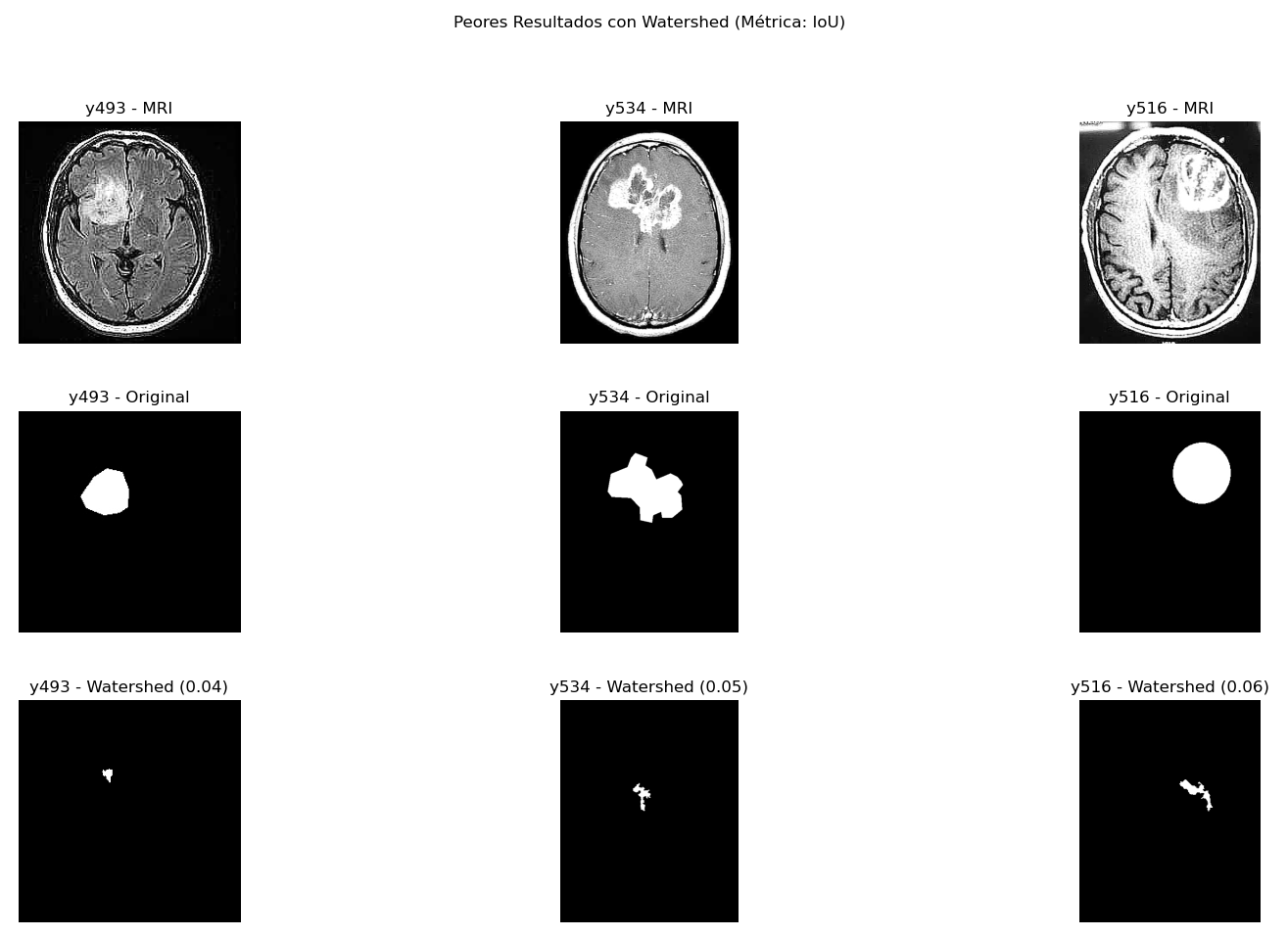
Peores casos Watershed
Estos peores casos ocurren cuando se pretenden seleccionar varias regiones para poder obtener lo máximo del tumor posible o cuando una región es demasiado acotada y el resto muy abarcativas. Fundamentalmente existen tumores que, al contener ruido o ser de baja resolución, hacen que el algoritmo lo divida en muchas regiones y no en una sola, luego estas regiones contienen partes del cerebro que para la segmentación no nos son útiles y esto causa que el tumor segmentado sea o muy acotado o demasiado extendido. Un ejemplo puede ser y509 (dice 19%) donde incluso seleccionando varias regiones seguimos sin abarcar la mayoría del tumor:
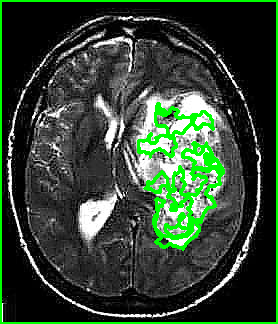
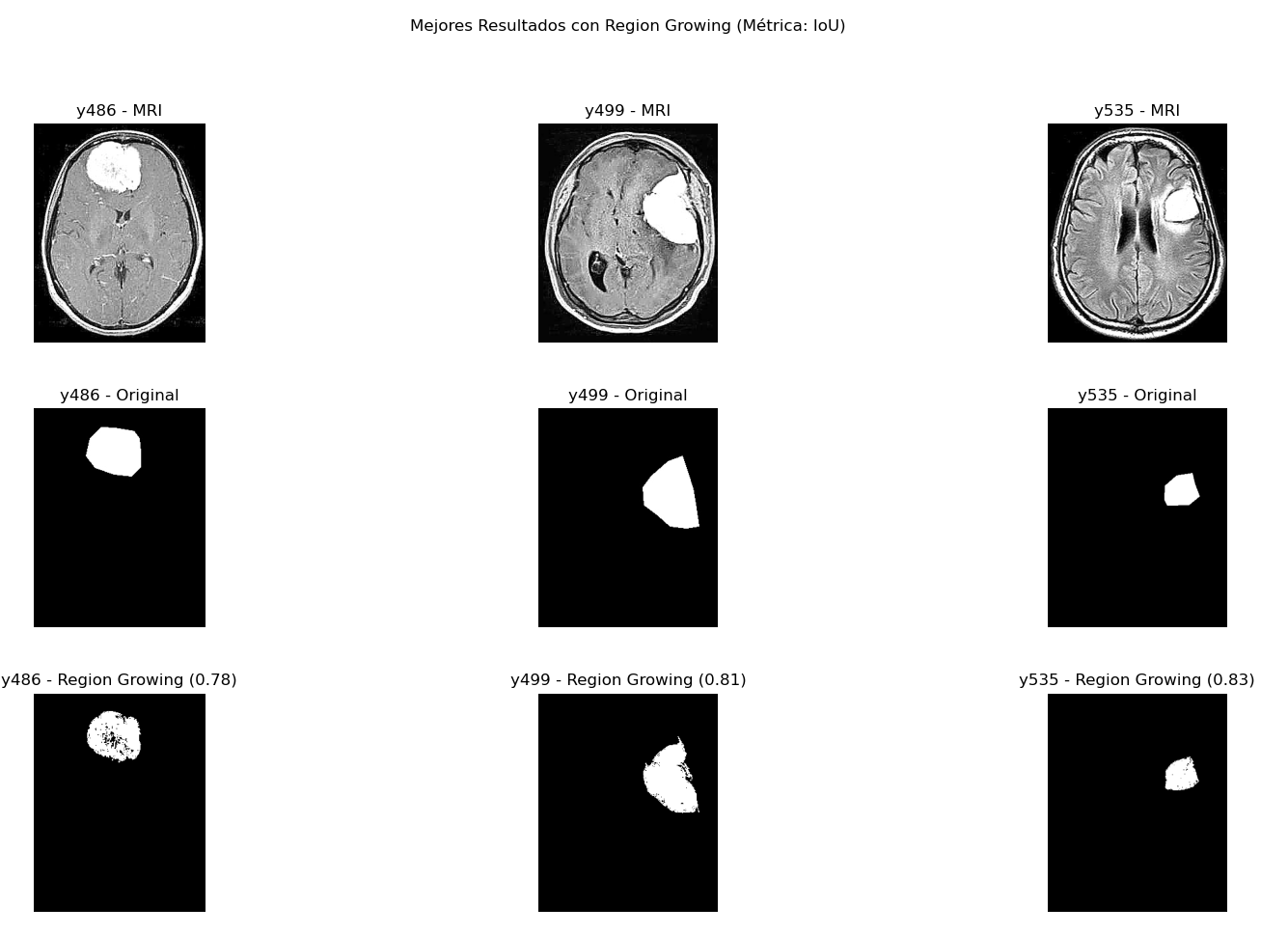
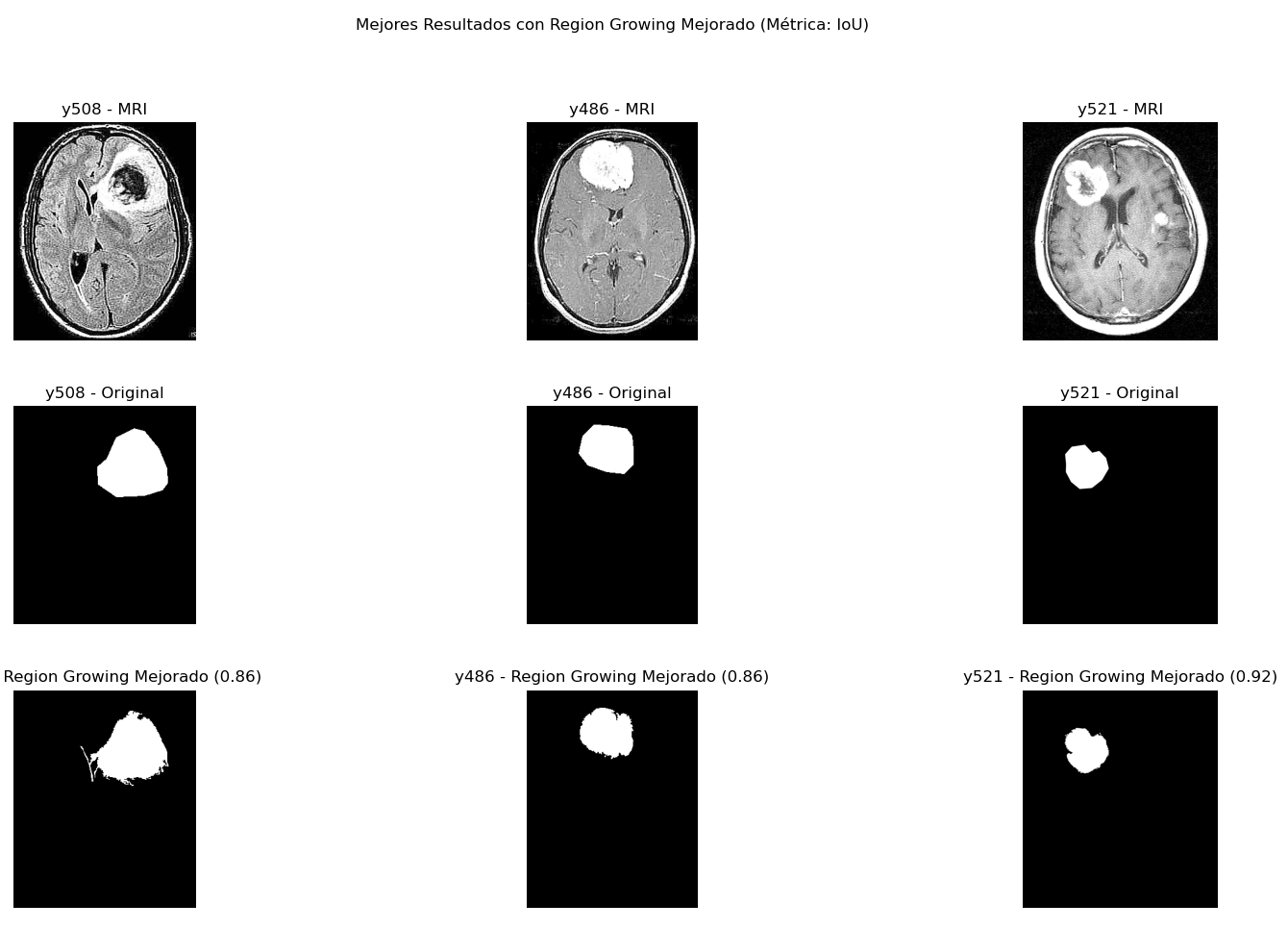
Mejores casos Region Growing
En particular este método repite un patrón con Watershed y es que si el tumor está aislado da resultados excelentes, en particular cuando el tumor tiene una luminosidad alta se logran contornos que son incluso mejores que los de la máscara original. Esto es de esperarse pues se inicia en un punto semilla y se expande a sus vecinos siempre que se cumpla con un umbral; particularmente en estos mris donde el tumor es muy luminoso este umbral se cumple y se detecta la totalidad (o casi del tumor). Un ejemplo puede ser y535 (dice 91%) (máscara region growing - máscara real):

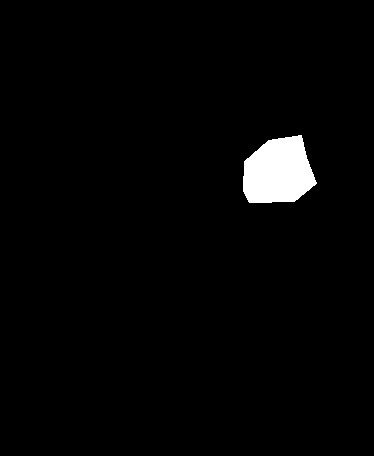
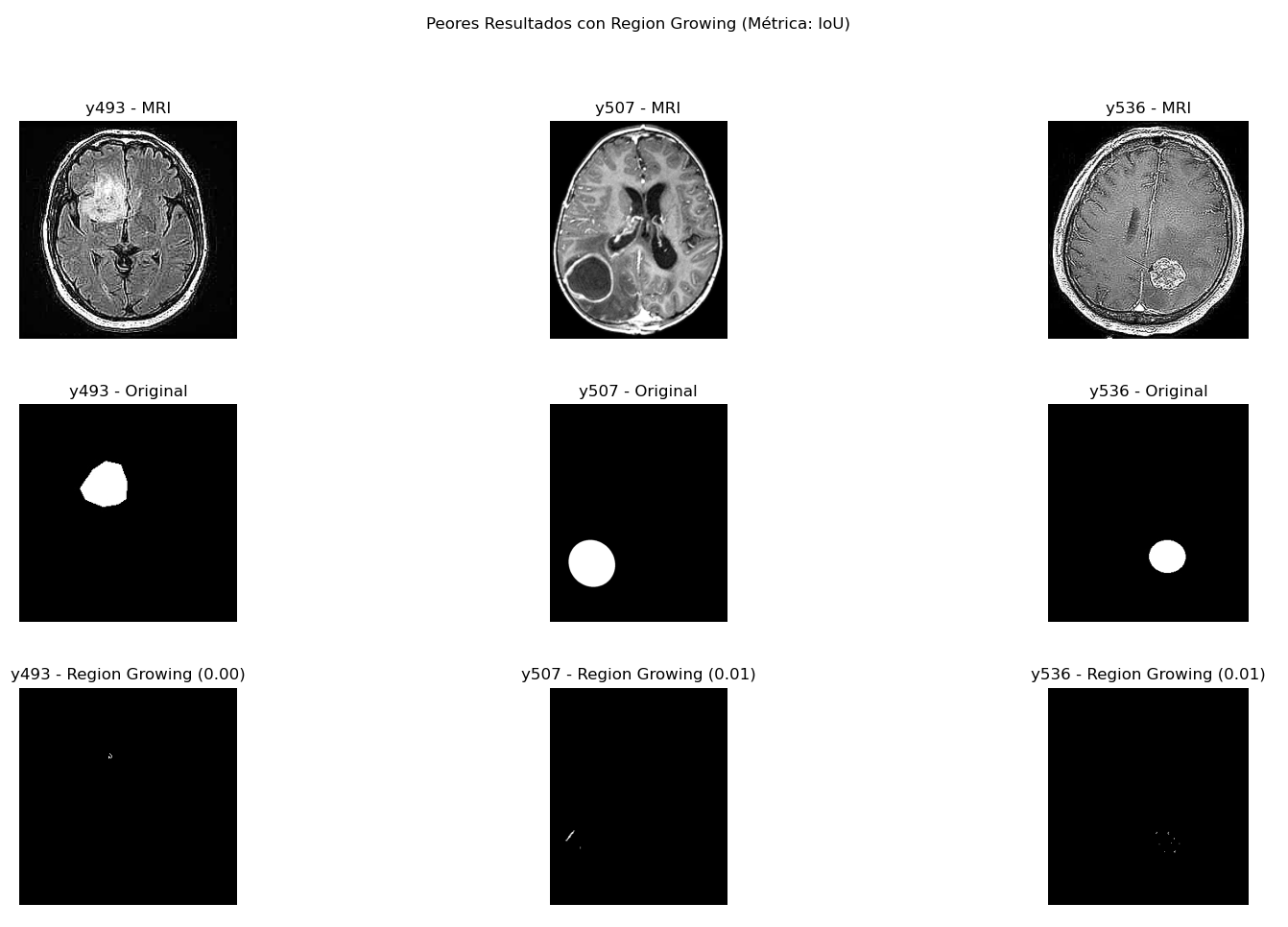
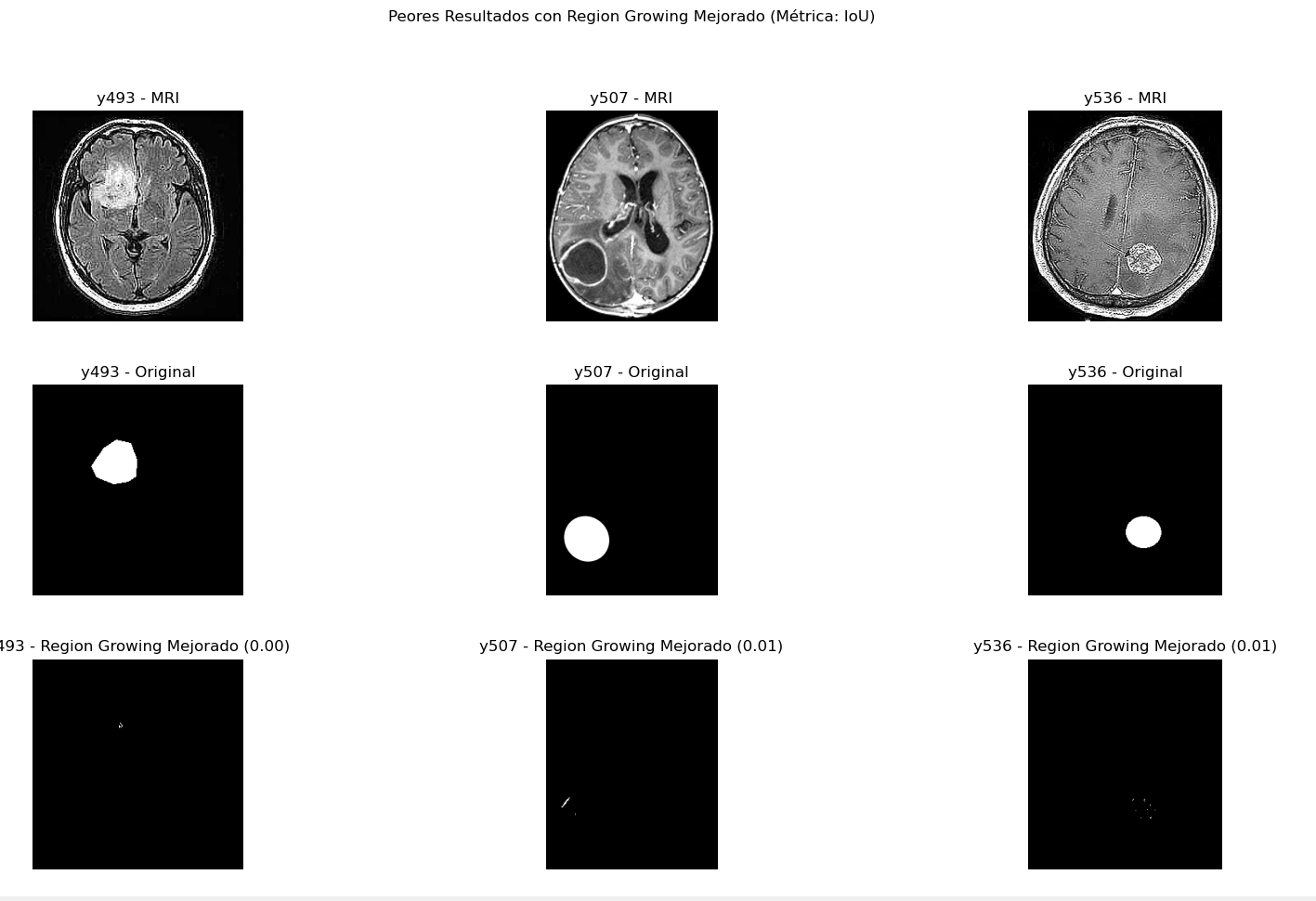
Peores casos Region Growing
Incluso en la máscara previamente presentada como una de las de mejor resultado podemos observar la principal debilidad del algoritmo que es el ruido en los tumores o la presencia de grises que superan el umbral establecido. En particular se obtienen resultados muy malos cuando el tumor tiene el núcleo de una tonalidad y la periferia de otra. El algoritmo no se adapta a poder detectar ambas regiones y eso causa tener resultados como y508 (dice 58%):
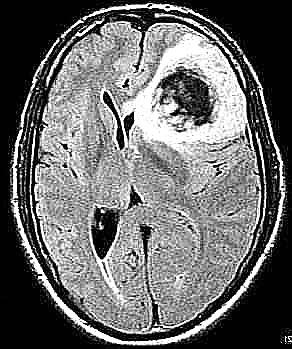

donde aunque la periferia está bien detectada, el centro no lo está.
Casos donde Region Growing Mejorado supera a Region Growing
Resonancias como y508 son el principal motivo de implementar este sub-método. En particular si rellenamos los “huecos” de este tumor (en la realidad médica no existen), logramos tener un tumor que respeta el contorno del original pero sin partes vacías en la máscara, haciendo que la comparación con la original sea mucho mejor. En particular el caso de y508 pasamos de un dice de 58% con Region Growing estándar a un 92% con esta implementación (máscara r.g.m - máscara real):


Casos donde Region Growing Mejorado empeora a Region Growing
Notar que, en las 60 resonancias analizadas en estos métodos, solo hubo un caso donde Region Growing Mejorado empeora a Region Growing y es cuando en la máscara con el método estándar estamos segmentando la periferia de la cabeza. En particular es la imagen y538 (mri - máscara region growing - máscara region growing mejorado):
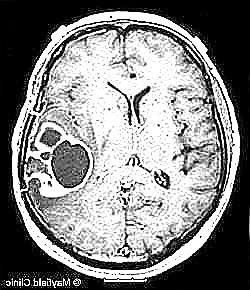
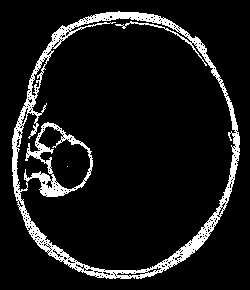

Esta puede ser considerada otra debilidad de Region Growing y es que en esta resonancia la periferia del tumor toma el mismo color que la periferia de la cabeza y eso hace que lo tome como parte del tumor. Luego si se rellenan los contornos trivialmente se obtiene una máscara casi completamente marcada que claramente es incorrecta. En particular pasamos de un dice de 23% a uno de 17% (en uno marcamos muy poco y mal, y en el otro marcamos demasiado).
Método con mejor acierto
El método con mayor acierto fue Region Growing Mejorado, seguido por Watershed. En particular podemos considerar Region Growing Mejorado el método más seguro a la hora de segmentar tumores ya que Region Growing suele marcar muy bien al menos la periferia del tumor y, salvo casos muy concretos como el anteriormente visto, rellenar el contorno aplica sensibles mejoras a los índices. Watershed se mantiene una buena opción cuando la región es claramente visible o se tienen tumores más oscuros y con más variedad que, como vimos previamente, Region Growing no detecta bien.
En particular el dice promedio de Watershed terminó siendo del 48% y el de Region Growing mejorado un 67%.
También creo que es pertinente mencionar que en 54 de las 60 imágenes obtenemos resultados de al menos un 50% de acierto Dice utilizando alguno de estos dos métodos y más de un 80% en 37 de los 60. Luego si se combinan ambas técnicas es seguro que se puede llegar a un buen resultado, también hay que tener en cuenta que involucran una interacción humana que influencia el resultado; evidentemente alguien que es experto en la materia va a poder segmentar los tumores con una mayor precisión que nosotros.
Dataset con máscaras mal hechas
Es importante aclarar que el dataset no incluye máscaras exactamente precisas, creo que esto hace que los resultados obtenidos destaquen aún más pues existen casos donde la máscara generada por los métodos semiautomáticos es, al ojo humano, más precisa que la dada por el dataset. Esto también se debe a que, mientras que algunos tumores cuentan con todos los puntos para formar un polígono, otros tienen la ecuación de una circunferencia, lo que lo hace mucho menos preciso.
Algunos ejemplos son:
-
y516 (máscara real circular, máscara region growing mejorado, mri):


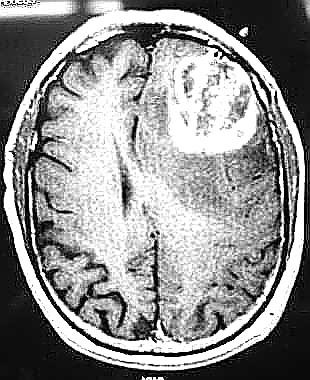
-
y508 (máscara real con baja cantidad de puntos para formar el polígono, máscara region growing mejorado, mri):


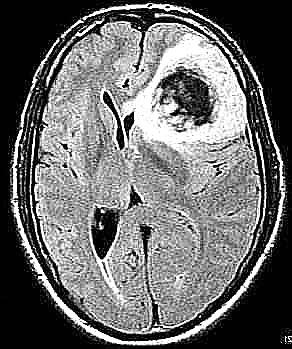
-
Modelo Watershed:
- Promedio de IoU: 0.34
- Promedio de Dice: 0.48
-
Modelo Region Growing:
- Promedio de IoU: 0.48
- Promedio de Dice: 0.61
-
Modelo Region Growing Mejorado:
- Promedio de IoU: 0.56
- Promedio de Dice: 0.67
-
Modelo UNet (total):
- Promedio de IoU: 0.39
- Promedio de Dice: 0.50
-
Modelo UNet (total, sin contar máscaras generadas vacías):
- Promedio de IoU: 0.46
- Promedio de Dice: 0.59
Conclusiones
Basado en los resultados proporcionados, se pueden hacer varias conclusiones sobre la efectividad de los modelos de segmentación semi automática para la detección de tumores cerebrales.
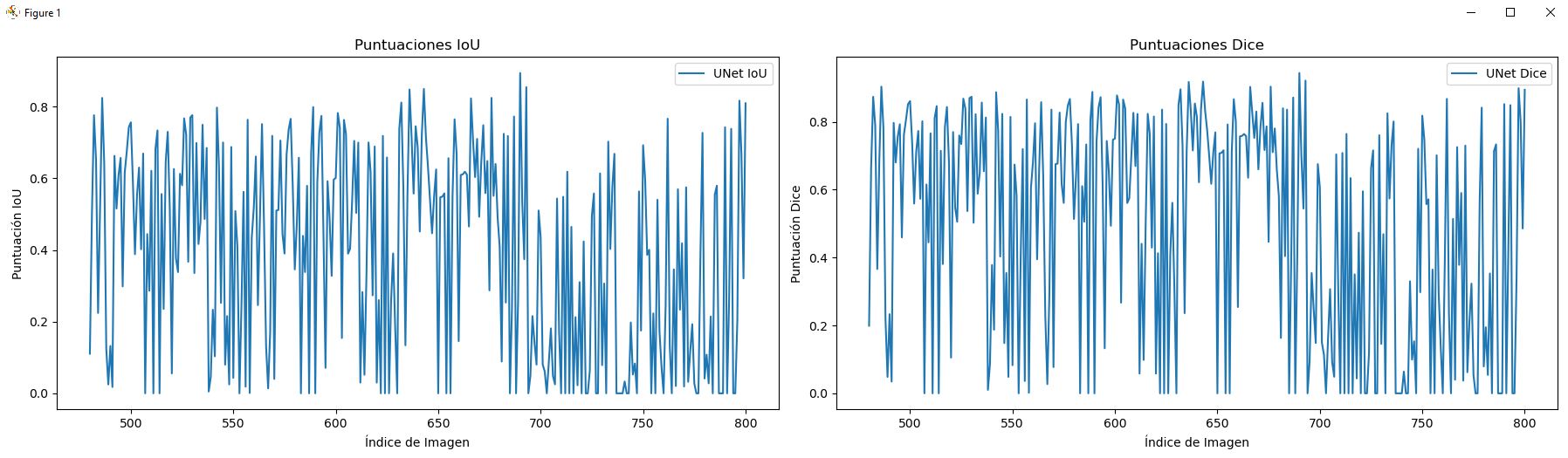
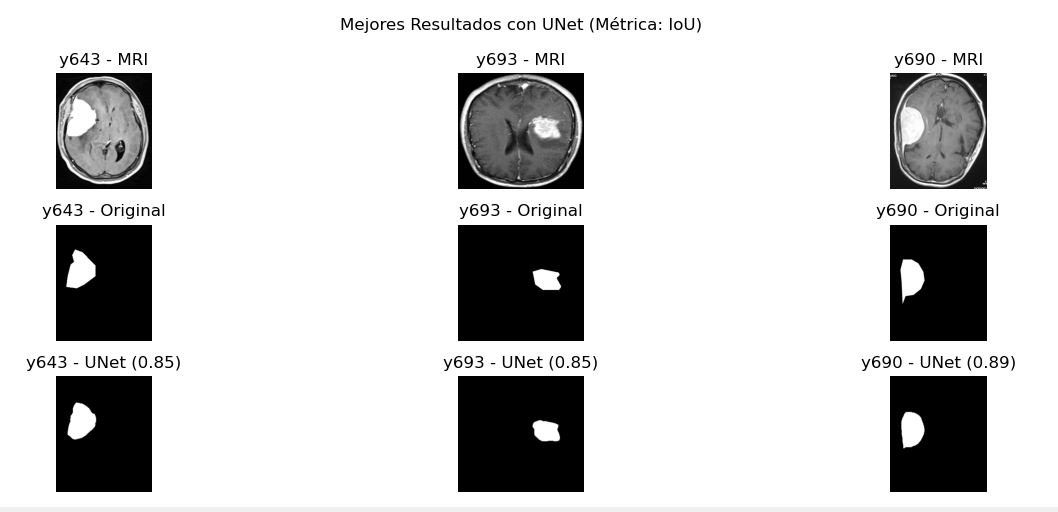
UNet
Sobre este modelo de redes neuronales, se puede concluir que los resultados obtenidos no son malos. En particular hay que tener en cuenta que el dataset con el que contamos no es tan amplio (se entreno con una base de 480 imágenes) y una cantidad de epochs no tan amplia (25). También es destacable que hubo muchas resonancias a las que no pudo segmentarle ningún tumor, muy probablemente debido al entrenamiento reducido del modelo. Cuando sí detecta algo para segmentar lo detecta bien con promedio 0.6 dice, que no es un mal resultado.
Comparación de Métricas IoU y Dice
Tanto las métricas IoU como Dice son indicadores de la calidad de la segmentación. La métrica Dice suele ser más indulgente y tiende a ser mayor que IoU porque se enfoca más en la superposición entre las máscaras predictiva y verdadera. Las mejoras en las métricas IoU y Dice indican una mejor superposición y, por tanto, una segmentación más precisa.
Rendimiento del Modelo Watershed
Los resultados del modelo Watershed son los más bajos en comparación con los otros modelos, con un promedio de IoU de 0.34 y Dice de 0.48. Esto sugiere que este método tiene dificultades para capturar con precisión la región del tumor.
Mejora con el Modelo Region Growing
El modelo Region Growing muestra una mejora significativa respecto a Watershed, con un promedio de IoU de 0.48 y Dice de 0.61. Esto indica que este método es más eficaz para segmentar los tumores cerebrales, probablemente debido a su capacidad para seguir los contornos del tumor de manera más precisa.
Efectividad del Modelo Region Growing Mejorado
El modelo Region Growing Mejorado tiene los mejores resultados, con un promedio de IoU de 0.56 y Dice de 0.67. Esto sugiere que las mejoras aplicadas a la técnica de region growing han resultado en una segmentación más precisa y fiable.
Tendencia de Mejora
Hay una clara tendencia de mejora al pasar de Watershed a Region Growing y finalmente a Region Growing Mejorado. Esto sugiere que las técnicas de segmentación que incorporan mejoras o refinamientos específicos pueden resultar en una mayor precisión y mejor rendimiento en la segmentación de tumores cerebrales.
En resumen, las técnicas de segmentación basadas en region growing, especialmente cuando se mejoran, muestran un mayor potencial para la detección precisa de tumores cerebrales en comparación con el método Watershed.
Conclusiones de Métricas IoU de U-Net y Métodos de Segmentación Semiautomáticos
| Método | Promedio IoU | Mejor IoU | Peor IoU |
|---|---|---|---|
| U-Net | 0.39 | 0.89 | 0.0 |
| Watershed | 0.34 | 0.84 | 0.04 |
| RG | 0.48 | 0.83 | 0.0 |
| RG Mejorado | 0.56 | 0.92 | 0.0 |
Comparación General de Métodos
RG Mejorado es el método más robusto con el mejor promedio, mejor IoU y un rendimiento consistente. RG también es fuerte con un buen promedio y mejor IoU. U-Net y Watershed tienen promedios más bajos y el peor IoU para U-Net es 0.Tendencias Observadas
RG Mejorado muestra el mejor rendimiento global. RG es una opción sólida con buen rendimiento. U-Net y Watershed necesitan ajustes para mejorar.Recomendaciones
RG Mejorado es ideal para alta precisión y consistencia. RG es una opción viable si el modelo mejorado no está disponible. U-Net y Watershed podrían beneficiarse de mejoras.Aunque U-Net tiene un buen "mejor IoU", su promedio es más bajo y su peor IoU indica inconsistencias. Para mejorar el rendimiento de U-Net, se puede ser recomendable aumentar el número de épocas de entrenamiento, usar mejor capacidad computacional y ampliar el tamaño del dataset. Estas mejoras ayudarían a U-Net a lograr un rendimiento más consistente y preciso.
Acerca de...
Esta pagina se realizó como entrega del proyecto final del curso Tratamiento de Imagenes.
Autores:
Lucas Ausquiz: lucas.ausquiz@fing.edu.uy
Wilder Peña: wilder.pena@fing.edu.uy
Santiago Cancela: santiago.cancela@fing.edu.uy
Referencias:
Segmentación UNet con tensorflow
Using U-Net network for efficient brain tumor segmentation in MRI images